Per secoli, la legge di gravità di Newton ha funzionato magnificamente, ma nessuno sapeva perché. Ecco come l’ha poi spiegata Einstein.
Una delle leggi scientifiche più rivoluzionarie della storia fu proposta per la prima volta da (no, non da Einstein) Isaac Newton nel XVII secolo: la legge di gravitazione universale. In parole povere, ipotizzava che tra tutte le masse dell’Universo, ci fosse una forza attrattiva che agiva su entrambe: la gravità. Ma quali erano le proprietà di questa forza? Secondo Newton, doveva:
- essere completamente universale, tra tutti gli oggetti dotati di massa;
- essere proporzionale alla massa di ciascun oggetto, moltiplicata insieme;
- essere istantanea e attraversare le grandi distanze che separano questi oggetti a velocità infinita e illimitata,
- e doveva anche indebolirsi con l’aumentare della distanza, diminuendo in proporzione al quadrato della distanza che separava questi oggetti. Ciò ha portato a quella che i fisici chiamano legge di forza dell’inverso del quadrato: se la distanza che separa due oggetti qualsiasi è data da r, allora la forza tra quei due oggetti è proporzionale a ~1/ r² .
Perché era una legge del quadrato inverso
Newton fu in grado di evidenziare molte proprietà convincenti di questa legge del quadrato inverso, tra cui il fatto che portava a orbite chiuse ed ellittiche, consentiva di derivare da essa tutte le leggi di Keplero sul moto planetario e che portava a pianeti sferoidali in cui gli oggetti cadevano sempre “giù” verso i loro centri. Ma una delle grandi domande era: perché era una legge del quadrato inverso? Perché questa forza era proporzionale a ~1/ r ², invece di qualsiasi altra possibilità? Perché quell’esponente nell’equazione era “2” piuttosto che un altro numero? Per centinaia di anni non lo abbiamo saputo. Poi è arrivato Einstein e ha dimostrato che non poteva essere altrimenti.
Cosa capì Einstein
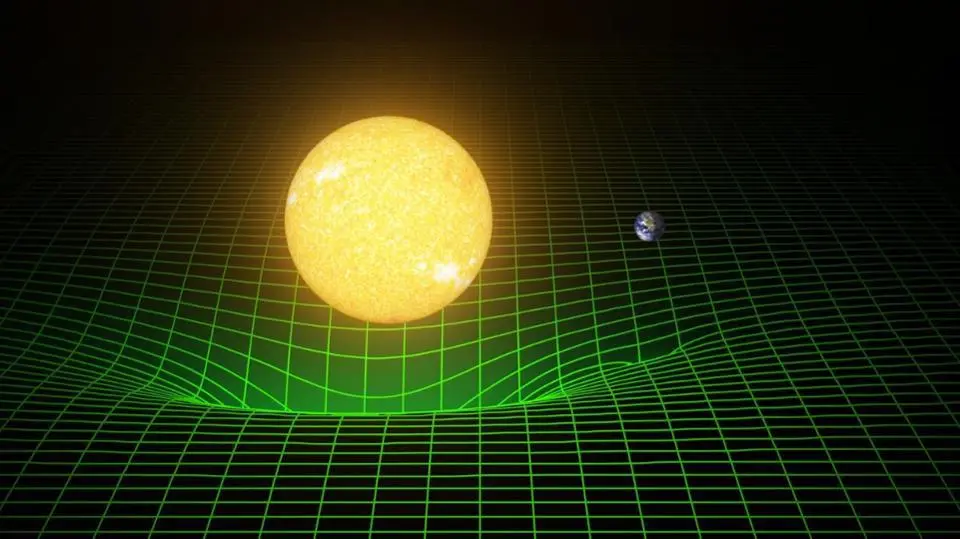
Quando arrivò Einstein, il suo grande problema con la gravità newtoniana era che non aveva senso nel contesto di una delle sue grandi scoperte del 1905: la nozione che non esistesse qualcosa come “spazio assoluto” o “tempo assoluto”, ma solo una combinazione unificata dei due, lo spaziotempo. La spiegazione è semplice se ci pensi. Per prima cosa, pensa al Sole: una grande sfera di materiale caldo che emette luce. Quando la luce emana dalla fotosfera del Sole (i suoi strati più esterni), non si propaga solo nello spazio; si diffonde anche mentre si allontana dalla sorgente. Il Sole è una sfera e la luce che ne deriva si propaga sfericamente verso l’esterno: in tutte e tre le dimensioni.
Il percorso della luce
Mentre questa luce si diffonde in una sfera, dobbiamo capire che non sta riempiendo la sfera di luce, che sarebbe un volume tridimensionale, ma piuttosto che si muove verso l’esterno in un guscio sferico: su un’area bidimensionale, come la superficie di un globo. Mentre si propaga più lontano dal Sole, la luce che ricevi su una qualsiasi quantità di area data diminuisce, poiché l’area di superficie di una sfera è data da 4π r ². Un pianeta che è due volte più lontano dal Sole di un altro riceve solo un quarto della luce per unità di area; un pianeta che è tre volte più lontano riceve solo un nono della luce per unità di area.
Esistono altre dimensioni?
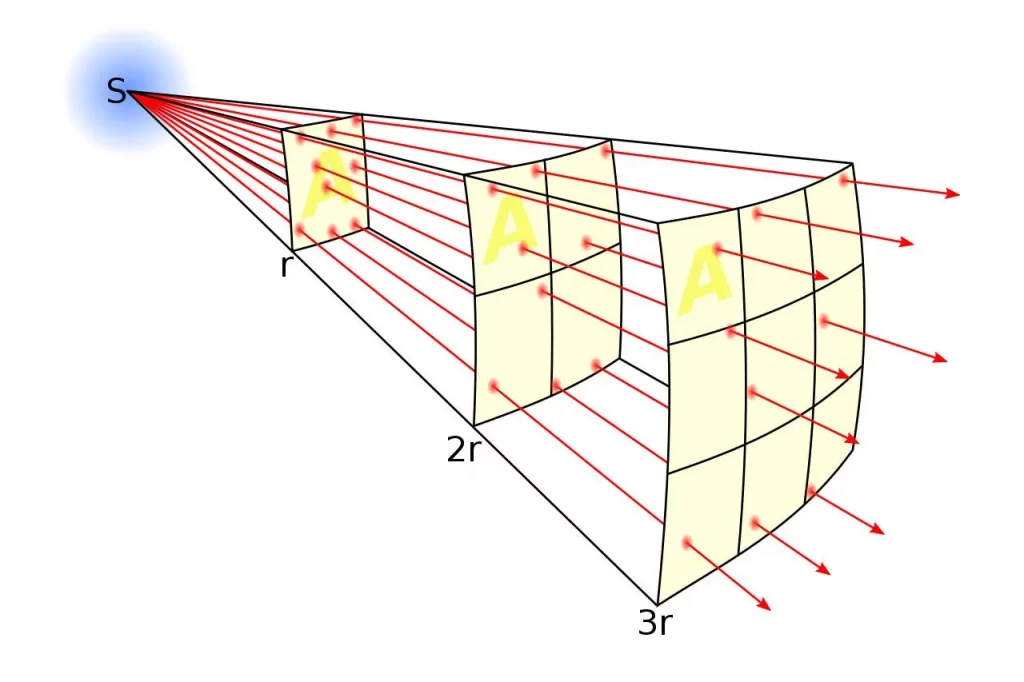
Fu attraverso una serie di esperimenti che Einstein, alla fine, fu in grado di spiegare la legge di forza dell’inverso del quadrato (vale a dire, ~1/ r ²) della gravità. Se lo spazio e il tempo non fossero assoluti e la gravitazione non si propagasse istantaneamente, allora la gravità dovrebbe viaggiare a una velocità finita e propagarsi attraverso lo spazio per interagire con gli oggetti nelle sue vicinanze. E poiché i segnali che viaggiano attraverso lo spazio si diffondono all’interno di quello spazio, allora il numero di dimensioni all’interno del nostro Universo avrebbe determinato il comportamento della forza gravitazionale con la distanza, dove un Universo tridimensionale implicava esattamente una legge di forza di ~1/ r ².
