Lo scienziato straordinario: al-Battānī

Per molti il più importante astronomo arabo. Al-Battānī ebbe grande risonanza tra coloro che l’hanno succeduto, in Oriente come in Occidente

Meglio conosciuto in Occidente come Albatenius o Albategnius, Abū ‛Abd Allāh Muḥammad ibn Jābir ibn Sinān al-Battānī (858 d.C. – 929 d.C.) trascorse la maggior parte della sua vita nella città di Raqqa, in Siria, dove effettuò le sue prime ricerche astronomiche. Operò negli osservatori di Raqqa e di Antiochia, dove poté applicare la sua conoscenza approfondita della scienza tolemaica e compiere numerosi progressi, che gli consentirono di apportare numerose annotazioni all’opera dello scienziato greco. Il suo trattato astronomico più importante, il Kitāb al-zīğ al-ṣābiʾكتاب الزيج ﺍﻟصابیء‎ (Il libro delle tavole astronomiche sabee), fu tradotto in latino già a partire dal 1100 circa, nonché, poi, direttamente in spagnolo per ordine del re Alfonso X di Castiglia, e rimase uno dei testi principali di riferimento per l’astronomia fino al Rinascimento. La sua opera è meglio conosciuta col titolo in latino De Scientia Stellarum (o De Rerum Stellarum). Agli inizi del XX secolo, l’illustre arabista italiano Carlo Alfonso Nallino ne ha realizzato un’eccellente edizione in tre volumi, con testo in latino e in arabo, nota come Opus astronomicum.

I calcoli sorprendenti di al-Battānī

Al-Battānī non soltanto migliorò il lavoro di Tolomeo con delle correzioni alle sue tavole sulla luna e i pianeti (che integrò con una descrizione più accurata dei loro moti); le differenze con lo scienziato greco sono numerose. Ad esempio, contrariamente a quanto sostenuto da Tolomeo, dimostrò la possibilità delle eclissi anulari di sole provando la variazione del diametro angolare della nostra stella. Ma, soprattutto, la sua eccezionalità sta nella precisione quasi esatta di alcuni calcoli da lui effettuati:

• Calcolando l’eccentricità dell’orbita solare – che secondo Tolomeo era costante nel tempo – scoprì che dall’epoca di Ipparco essa aveva subito una diminuzione da 0,0207638 a 0,017326. Si tratta, in effetti, di un calcolo di eccezionale precisione, dato che la misura esatta al tempo era di 0,016771; 
• Osservando, invece, un aumento di 16° e 47’ nella longitudine dell’apogeo dell’orbita solare dai tempi di Tolomeo, ne dedusse, diversamente dallo scienziato greco, che gli apsidi solari non sono immobili e dimostrò che l’orbita solare segue il movimento degli equinozi (precessione), determinando i valori di quest’ultimo in 54,5” all’anno, ovvero superando di soli 4,5” il suo valore esatto; 
• Calcolò anche l’inclinazione dell’eclittica in 23°e 35’, con soli 41” di differenza con il valore che aveva all’epoca e, inoltre, al contrario di Tolomeo, ipotizzò che l’inclinazione subisce una lenta variazione nel tempo; 
• Infine, nel determinare la durata di un anno solare, al-Battānī superò i calcoli di Ipparco di Nicea stabilendone la durata in 365 giorni, 5 ore, 46 minuti e 24 secondi, ovvero con una differenza di solo 2 minuti e 22 secondi rispetto al suo valore corretto!

Contributo alla trigonometria e influenza sugli scienziati occidentali

Per i suoi calcoli astronomici, al-Battānī fece ampio utilizzo della trigonometria piuttosto che dei metodi geometrici, ottenendo in questo modo di migliorare i calcoli di Tolomeo. Inoltre, con le sue considerazioni sulla proiezione ortografica della sfera riuscì ad apportare nuove soluzioni alla trigonometria sferica. Tali soluzioni riecheggiano in parte nel lavoro del matematico e astronomo tedesco Regiomontano. Produsse anche un catalogo di 489 stelle, mentre il suo studio dettagliato delle eclissi solari e lunari fu impiegato successivamente da Dunthorne, nel XVIII secolo, per la sua ricerca sull’accelerazione secolare del moto lunare. Lo stesso Copernico, nel suo De Revolutionibus Orbium Coelestium, cita l’opera al-Battānī in almeno 23 casi, ma tanti altri scienziati occidentali hanno riconosciuto la sua importanza, tra questi: Tycho Brahe, Galileo e Keplero. Anche a lui, così come ad al-Khwārizmī, è stato dedicato un cratere lunare.

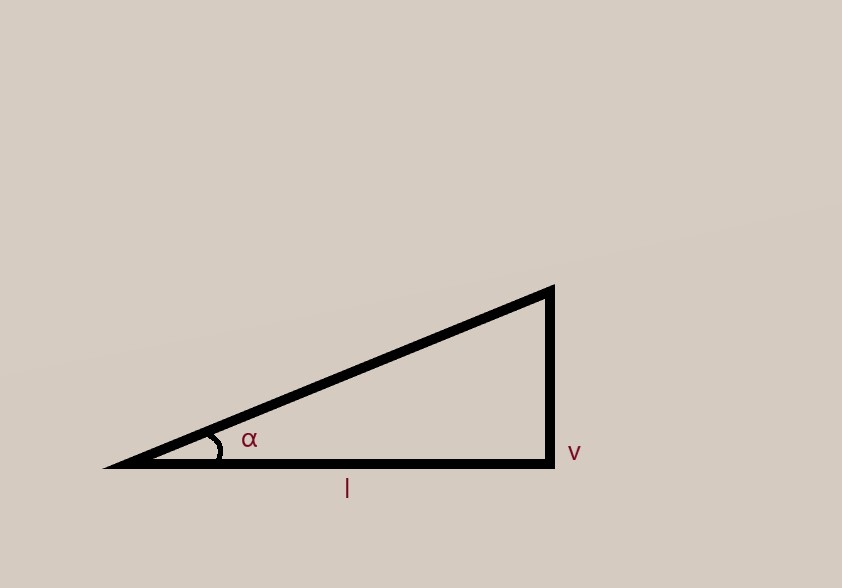
Per calcolare l’elevazione (α) del Sole sull’orizzonte al-Battānī si servì di un’asta verticale (v) e della lunghezza della sua ombra proiettata (l) impostando la seguente relazione: l = v cos α /sen α, da cui l = v cotg α, che giunse a risolvere preparando una una tabella di cotangenti (tavola delle ombre) per ogni grado da 1° a 90°.

Riferimenti:

• Beas Portillo Carlos, Las matemáticas y la astronomía en el mundo musulmán según el catálogo de Muhammad lbn Ishak an-Nadîm, Pontificia Universidad Católica del Perú, ARETÉ revista de filosofía Vol. VIII. N2 1, 1996.
• MAGHOUT, Khaled. “AL-BATTĀNĪ UN GRAND ASTRONOME ET MATHÉMATICIEN ARABE.” Bulletin D’études Orientales, 41/42, 1989, pp. 55–58. JSTOR, www.jstor.org/stable/41608313. Accessed 20 Mar. 2021.
• https://www.britannica.com/biography/al-Battani
• https://www.treccani.it/enciclopedia/albatenio_%28Enciclopedia-Italiana%29/
• www.wikipedia.org